Quantification of quantum chaos using OTOCs
Semester Project
The notion of chaos is central to understanding some of the fundamental aspects of statistical mechanics such as ergodicity and thermalization. Chaos in classical mechanics is well defined as the sensitivity of a system to arbitrarily small changes of its initial conditions, charecterized by Lyapunov exponent e.g. the growth rate of separation of two trajectories that are nearby at initial time. On the other side the definition and characterization of chaos in unitary quantum dynamics is a topical subject of investigation, in a recent developement chaos in quantum systems was charecterized as the spatio-temporal growth rate (“quantum Lyapunov exponent”) of an out of time order correlation(OTOC) of non compatiable local operators. In classical mechanics there is no bound on the Lyapunov exponent but recently a bound on the “quantum Lyapunov exponent” was argued that depends on Temperature of the system and the Planck constant.
This bound can be understood by visualizing a semi-classical chaotic dynamics as a thermal wave packet of a single particle moving in a high dimensional phase space trajectory; where the bound appears as the impossibility to scatter the wave packet due to the curvature of the trajectory caused by a complex chaotic landscape over characteristic lengths smaller than the thermal deBroglie wavelength. This semi-classical picture encourages one to think the quantum bound of chaos to be underpinned by the classical characteristics of a system and suggests the following property for a maximally chaotic system: the underlying classical system must have a spectra of chaotic length scales (trajectory curvatures) with no IR cut-off, such that even at the lowest possible energy the system has chaotic length scales below the deBroglie wavelength. Examples of such systems include various critical systems, specifically SYK model of quantum glasses , black holes are heavily investigated from this perspective. While this semiclassical picture gives some understanding based on quantum corrections on classical trajectories, it is still an open question how one can think about chaos in a purely quantum mechanical system where there is no concept of trajectory.
In this work we attempt to work towards these questions by studying various quantum mechanical systems and trying to understand the interrelation of “quantum Lyapunov exponent” and the classical Lyapunov exponent.
We calculated OTOC for various quantum mechanical systems (single particle) –Simple Harmonic Oscillator, particle in a box, stadium billiard, Inverse Simple Harmonic Oscillator, inverse square, coupled oscillator.
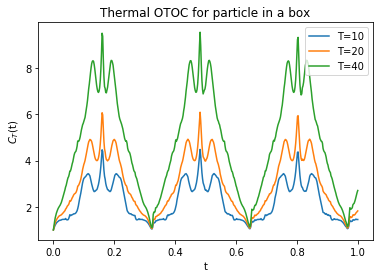
After that we calculate the OTOC for the inverse square potentials. A
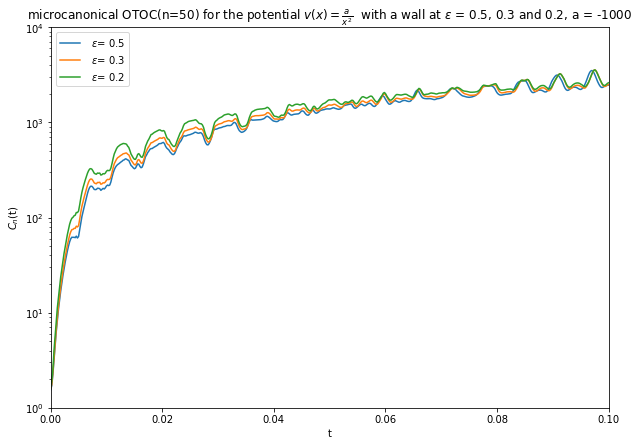
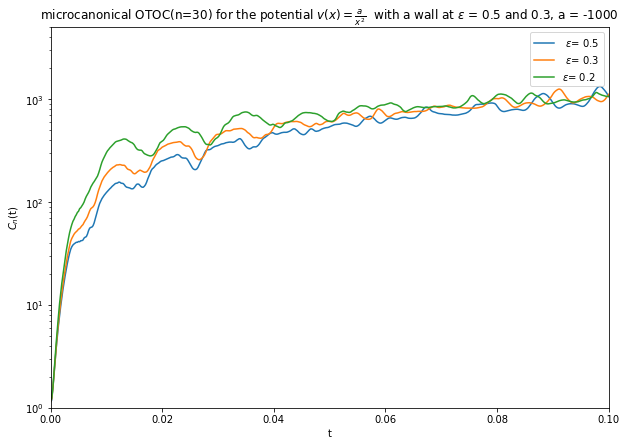
Here, you can see the polynomial growth of OTOC suggesting the presence of chaos!
Here is a overview of the chaos and scrambling:
| Comparison table | |||
|---|---|---|---|
| Dynamical systems | Scrambling | Chaos | Nature of OTOC |
| Particle in a box | not present | not present | Does not grow exponentially in time |
| Stadium billiard | not present | present | Does not grow exponentially in time |
| Harmonic oscillator | not present | not present | Does not grow exponentially in time |
| Inverted harmonic oscillator | present | not present | Grows exponentially in time |
| Coupled harmonic oscillator | present | present | Grows exponentially in time |