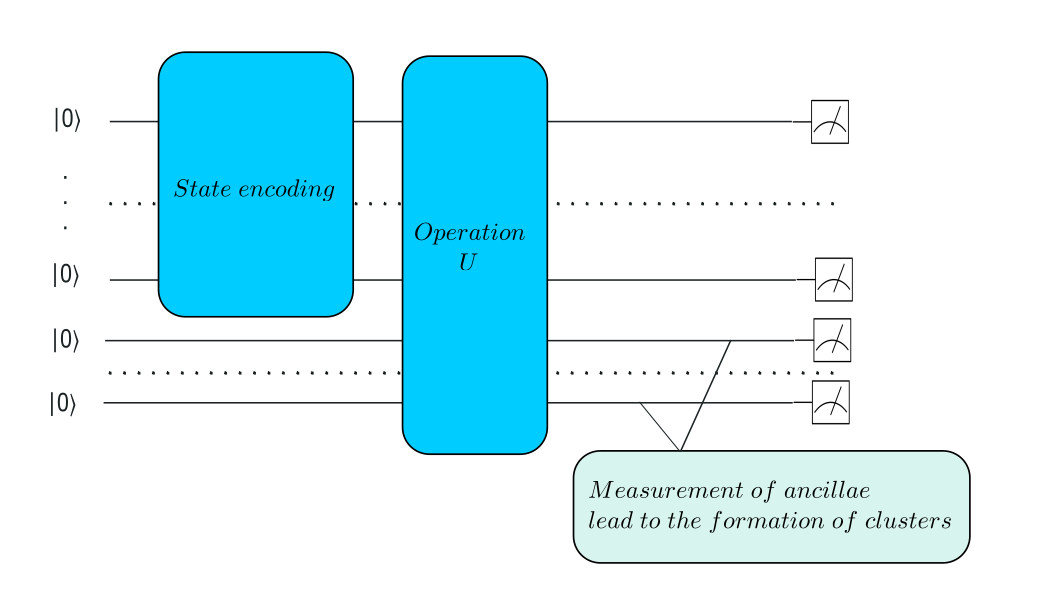
Solving CO problems through VQA and unsupervised clustering

How would you determine the ground state of a quantum system with no exact solution?

Dr. Sheldon Cooper

For my thesis, I joined lab of Prof. Prasanta Panigrahi at IISER Kolkata and worked on solving large scale combinatorial optimization problems through clustering methods.

Together, we developed two novel clustering algorithms, one being a quantum algorithm following divisive approach and the other being inspired by unsharp measurements. Following blocks show the workflow of developed algorithms.

Heirarchical Quantum Clustering Algorithm

    Input: {D_{k_1i}}, n, m
    Output:  k  clusters
    initialization
    Construct the state  |ψ>
    for num_clusters !=  k 
    |    apply  U  on n + m register if num clusters = k then
    |    |   Return: Output
    |    else
    |    |    further split the clusters by applying U or merege until num clusters = k
    |    end
    end

Unsharp measurement based Clustering Algorithm

    Input: {D_{k_1i}}, n
    Output: k clusters
    initialization
    Construct the superposed quantum state as described
    for cluster around point i do
    |    measure state unsharply around i if num clusters = k
    |    then
    |    |    Return: Output
    |    else
    |    |    re-center the next distance j at i and measure until num clusters = k
    |    end
    end

We implemented them on various datasest for the benchmarking purpose and found that it outperforms state-of-the-art quantum clustering algorithms as well as classical divisive clustering. Below are the results.

(Left) Dataset of 400 points generated using sklearn with noise ratio of 0.1. (Middle) Classification of the dataset using the traditional classical divisive clustering algorithm. (Right) Classification of the dataset using the QHCA. Different colors represent different clusters.

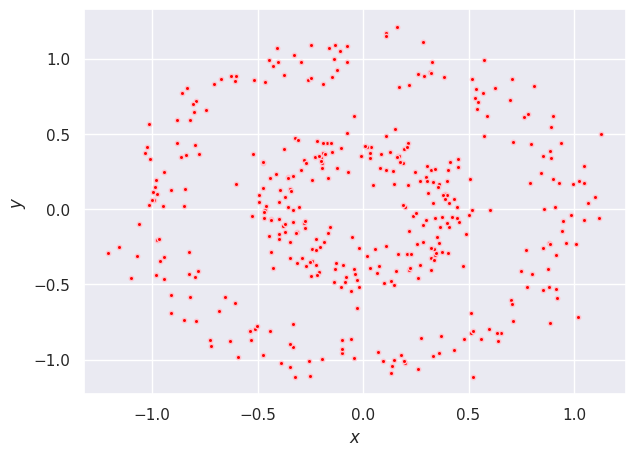
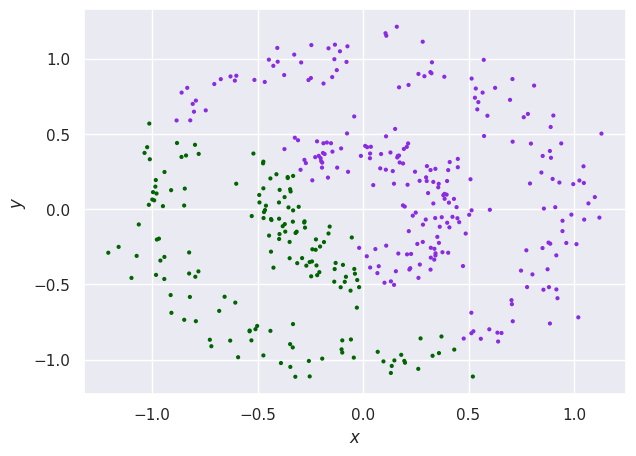
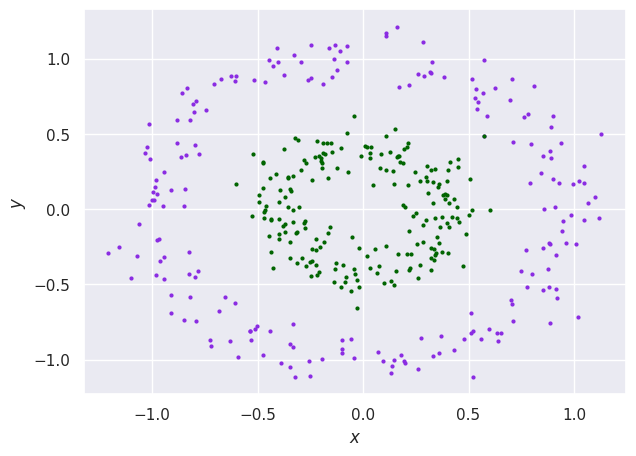
The main goal of thesis was to solve large scale graph problems like TSP; we employed two methods:

(i) one is implenting developed algorithms to cluster the nearby cities in TSP data.

(Left) Original TSP dataset of 130 cities (Right) Radially clustered data

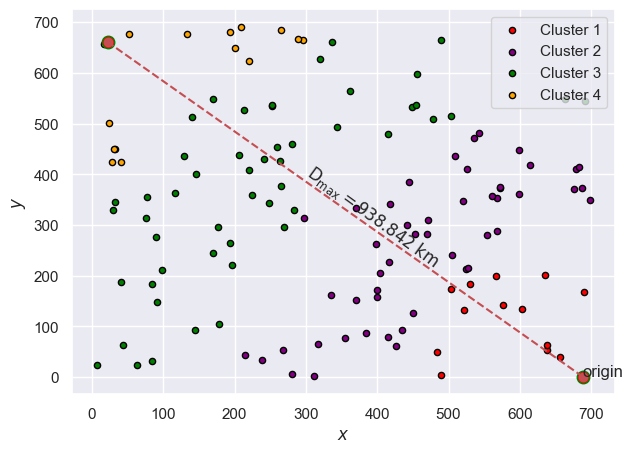
(ii) and the second using tensor networks.

In this paper, two novel measurement-based clustering algorithms are proposed based on quantum parallelism and entanglement. The Euclidean distance metric is used as a measure of ‘similarity’ between the data points. The first algorithm follows a divisive approach. The second algorithm is based on unsharp measure- ments where we construct the set of effect operators with a Gaussian probability distribution to cluster similar data points. One major advantage of both the pro- posed algorithms is that they are simplistic in nature and easy to implement. We have successfully applied both algorithms on a concentric circle data set where the classical clustering approach fails. It is found that the presented clustering algorithms perform better than the classical divisive one; both in terms of clus- tering and time complexity which is found to be O(kN(logN)^2) for the first and O(N^2) for the second one. Alongside, we also implemented the algorithm on the Churrtiz data set of cities and the Wisconsin breast cancer dataset where we found an accuracy of approximately 97.43% which for the latter case is achieved by the appropriate choice of the variance of the Gaussian window.

Solving CO problems through VQA and unsupervised clustering

Heirarchical Quantum Clustering Algorithm

Unsharp measurement based Clustering Algorithm

References

2023